

An integral that looks quite innocent... and it really kind of is.
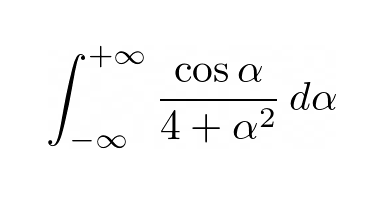
Recall that $\cos\alpha = \Re(e^{i\alpha})$, then bring the $\Re$ operator to the outside. The integral turns into a form we can use the Residue Theorem (and subsequently Jordan’s Lemma) to evaluate.
$$\int_{-\infty}^\infty\frac{\cos(\alpha)}{\alpha^2+4}~\mathrm{d}\alpha$$
Clearly, this integral can’t really be done with the elementary methods, so we’ll have to tackle this using something more “complex”. We know that the $\cos(\alpha)$ on top can be simplified with the complex function $e^{i\alpha}$ like so: $$\int_{-\infty}^{\infty} \frac{\Re(e^{i\alpha})}{\alpha^2+4} ~ \mathrm{d}\alpha$$
From here, because the $\cos(\alpha)$ is the only part of the integrand that requires a real part operator, we can pull the operator to the outside. We can then define a contour in the complex plane, $C$, to be the upper half of the complex plane, and now integrate along that: $$\Re\left(\oint_{C}\frac{e^{i\alpha}}{\alpha^2+4}~\mathrm{d}\alpha\right)$$
Now let’s quickly factor the bottom to prepare ourselves to apply the residue theorem: $$\Re\left(\oint_{C}\frac{e^{i\alpha}}{(\alpha+2i)(\alpha-2i)} ~ \mathrm{d}\alpha \right)$$
We can see the residues are $\pm 2i$, but we’re only interested in the one in our residue $C$, so only $2i$ is relevant to us. The residue becomes: $$\lim_{\alpha \to 2i}\frac{e^{i\alpha}}{\alpha+2i} ~=~ \frac{e^{-2}}{4i} ~=~ \frac{-i}{4e^2}$$
And now we apply the residue theorem: $$\Re\left({2\pi i \cdot \frac{-i}{4e^2}}\right)= \Re\left(\frac{2\pi}{4e^2}\right) = \boxed{\frac{\pi}{2e^2}}$$