

An infinite sum that’ll surely make you want to hate trig
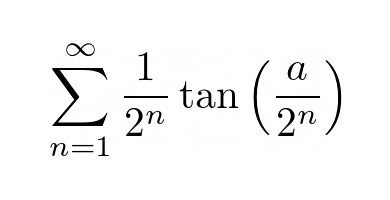
Not sure if this was actually taught in trig, but here are two simple half-angle identities: $$\tan\frac{\theta}{2} = \csc\theta - \cot\theta = \frac{1}{\csc\theta + \cot\theta}$$ This stems sines and cosines and it’s listed here if you want more context on these identities.
We can express our sum in a simpler form, namely $\frac{1}{2}\tan\frac{a}{2}$, and then use the first identity to obtain: $$\frac{1}{2}\tan\frac{a}{2} = \frac{1}{2}\csc a - \frac{1}{2}\cot a = \frac{1}{2}\csc a + \frac{1}{2}\cot a - \cot a$$ Now we use the second identity to recognize that $\frac{1}{2}\csc a + \frac{1}{2}\cot a = \frac{1}{2}\cot\frac{a}{2}$ and then: $$\underline{\frac{1}{2}\tan\frac{a}{2} = \frac{1}{2}\cot\frac{a}{2} - \cot a.}$$
Situational identity? Yeah, it’s really kind of stupid. But it’s good to recognize that this can now become a telescoping series if we apply the identity to the sum.
$$\sum_{n=1}^{\infty} \frac{1}{2^n}\tan\left(\frac{a}{2^n}\right)$$
This sum depends a lot on knowledge of (you guessed it) trig identities. In this case, let’s consider the identity:
$$\frac{1}{2}\tan\frac{a}{2} = \frac{1}{2}\cot\frac{a}{2} - \cot a. $$
We can generalize this identity since we need the “n"th power of 2 and not just 2 itself:
$$\frac{1}{2^n}\tan\frac{a}{2^n} = \left(\frac{1}{2^n}\cot\frac{a}{2^n}\right) - \left(\frac{1}{2^{n-1}}\cot \frac{a}{2^{n-1}}\right). $$
From here, we can rewrite the sum:
$$\sum_{n=1}^{\infty} \left(\left(\frac{1}{2^n}\cot\frac{a}{2^n}\right) - \left(\frac{1}{2^{n-1}}\cot \frac{a}{2^{n-1}}\right)\right)$$
$$= \lim_{N \to \infty}\sum_{n=1}^{N} \left(\left(\frac{1}{2^n}\cot\frac{a}{2^n}\right) - \left(\frac{1}{2^{n-1}}\cot \frac{a}{2^{n-1}}\right)\right).$$
From here, we can notice that this resembles a telescoping series, so we can write out the first few terms and the last few: $$= \lim_{N \to \infty}\left(\frac{1}{2}\cot\frac{a}{2} - \cot a\right) + \left(\frac{1}{4}\cot\frac{a}{4} - \frac{1}{2}\cot\frac{a}{2}\right) + \left(\frac{1}{8}\cot\frac{a}{8} - \frac{1}{4}\cot\frac{a}{4}\right) +$$ $$\ldots +\left(\frac{1}{2^N-1}\cot\frac{a}{N-1} - \frac{1}{2^N-2}\cot\frac{a}{2^N-2}\right) + \left(\frac{1}{2^N}\cot\frac{a}{2^N} - \frac{1}{2^N-1}\cot\frac{a}{2^N-1}\right).$$
and the terms cancel out to become…
$$= -\cot a + \left(\lim_{N \to \infty}\frac{1}{2^N}\cot\frac{a}{2^N}\right).$$
Now we’re just left with a limit to evaluate, and it seems pretty hard… but worry not! As 3b1b once said, make the problem simpler (or something like that). So we’ll just make a quick substitution of $N = 2^N.$ With this, we can rewrite the limit:
$$\lim_{N \to \infty}\frac{1}{N}\cot\frac{a}{N}$$
With a small application of L’Hopital, the limit becomes simple:
$$= \lim_{N \to \infty}\frac{\cos\frac{a}{N}}{N\sin\frac{a}{N}}=\frac{1}{\lim_{N \to \infty}\frac{\sin\frac{a}{N}}{\frac{1}{N}}}=\frac{1}{\lim_{N \to \infty}-N^2\frac{-a}{N^2}\cos{\frac{a}{N}}}=\frac{1}{a}.$$
Since the final limit is independent of $N$ and will hold as long as $\lim_{N \to \infty} N = \infty$, the substitution holds as well and our final answer becomes: $$\boxed{-\cot{a} + \frac{1}{a}}.$$