

It's... quite hard, but still not pulling out your hair batshit insane :)
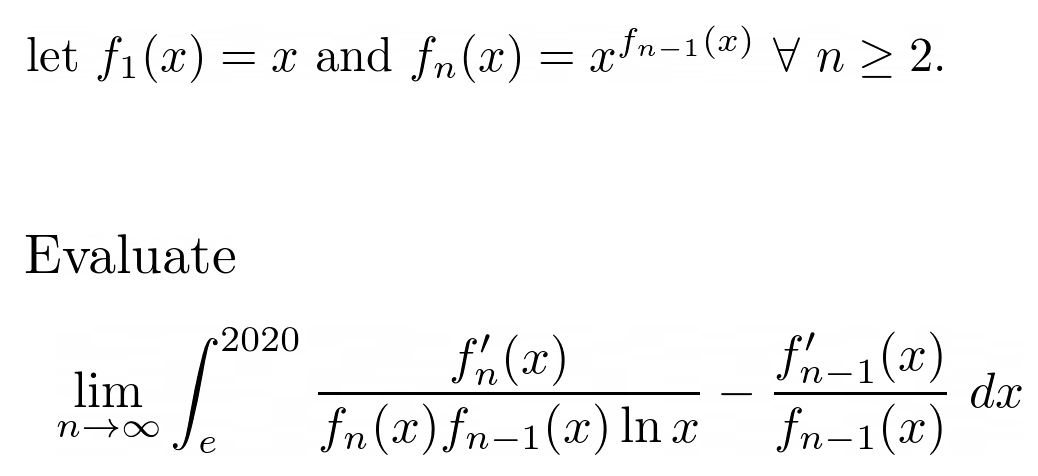
I guess I’ll just put this here from now on so it’s more legible and whatnot.
Let $f_1(x)=x$ and for every integer $n\geq 2$, define $f_n(x)=x^{f_{n-1}(x)}$. Evaluate $$ \lim_{n\to\infty}\int_e^{2020} \frac{f’n(x)}{f_n(x)f{n-1}(x)\ln x}-\frac{f’{n-1}(x)}{f{n-1}(x)}~dx $$
This is a weird one, but it helps to simplify things down a bit when we make n a low number so that the computations for derivatives and multiplying are still doable. Split the two parts of the integral (left and right of subtraction sign) and compute a couple examples for smaller n, then generalize as n approaches infinity and finally piece together what you have.
The integral ends up being quite nice, so if you’re having trouble evaluating the actual integral after getting rid of the recursive functions, you probably fucked up.
Let’s label some parts of the integral: $$ \lim_{n\to\infty}\int_e^{2020} \underbrace{\frac{f’n(x)}{f_n(x)f{n-1}(x)\ln x}}{(1)}-\underbrace{\frac{f’{n-1}(x)}{f_{n-1}(x)}}{(2)}~dx $$ We’ll look at $(2)$ first since it is easier. From one look at this you can probably tell that this calls for a fairly obvious u-substitution where $u = f{n-1}(x)$.
This side essentially becomes $$ \int \frac{1}{u} ~du=\ln(u) $$ where we’re ignoring the bounds until evaluating $(1)$, since this is a limit to infinity and this term would diverge if we were to evaluate it now. We can also ignore the absolute value sign on the ln since our bounds are strictly positive.
Substituting back u, we get that this term is just $$ \tag{2}\ln(f_{n-1}(x)) $$ Next, we can look at $(1)$. This is objectively the harder side, as we can’t substitute and there’s a weird product on the bottom. But we’ll start by expanding the numerator as derivatives are harder to figure out usually in sequences.
Let’s begin with a simpler example of the numerator when n = 2. We get that $f_2(x) = x^x$ and then $$ f_2’(x)=x^x(1+\ln x)=x^xx\ln x\left(\frac{1}{x\ln x}+\frac{1}{x}\right) $$ The reason we put it into the final form will be apparent later.
We can then do this again for n = 3 to see if we can continue the pattern, i.e. $f_3(x) = x^{x^x}$. These derivatives all use implicit differentiation: $$ \begin{align} f_3’(x)&=x^{x^x}\left(\frac{x^x}{x} + x^x\ln x(1+\ln x) \right)\newline &=x^{x^x}x^x\ln x\left(\frac{1}{x\ln x} +1+\ln x\right) \end{align} $$ Looking at the part not in parentheses, we can see the pattern for these will all follow some form that’s similar to: $$ f_n’(x)=f_n(x)f_{n-1}(x)\ln x(…) $$ If we look at our original fraction, we can see that things will cancel out pretty nicely: $$ \frac{\cancel{f_n(x)f_{n-1}(x)\ln x}(…)}{\cancel{f_n(x)f_{n-1}(x)\ln x}} $$
leaving us with just the stuff in parentheses. If we integrate that term when n = 2, we get $$ \int\frac{1}{x\ln x} + \frac{1}{x}~dx=\ln(\ln x) + \ln x $$
both of which are trivial integrals. Moving onto n = 3, $$ \int \frac{1}{x\ln x}+1+\ln x~dx =\ln(\ln x)+x\ln x $$
This will continue to follow the pattern, and the nth term will be $$ \ln(\ln x)+x^{x^{\cdots}} \ln x=\ln(\ln x)+f_{n-2}(x)\ln x $$
since for n = 2 we had 1 as the coefficient of ln(x), which is just f0(x), and for n = 3 we had x, which is just f1(x), and so on.
Thus, we can conclude our $(1)$ term is just $$ \tag{1}\ln(\ln x)+f_{n-2}(x)\ln x $$ Putting both parts together, we get the entire integral simplifies down to $$ \lim_{n\to\infty}\left[\ln(\ln x)+f_{n-2}(x)\ln x-\ln(f_{n-1}(x))\right]e^{2020} $$ Using the log property where $\ln x^a=a\ln x$ on the middle term, we can get $$ f{n-2}(x)\ln x=\ln\left(x^{f_{n-2}(x)}\right) $$ Then, using the fact that $\ln\left(x^{f_{n-2}(x)}\right) = \ln\left(f_{n-1}(x)\right)$ from our definitions of $f_n(x)$, this term and the rightmost term will cancel, leaving us with $$ \left[\ln(\ln x)\right]_e^{2020}=\boxed{\ln(\ln 2020)} $$
where the limit ends up vanishing as we cancelled out all terms with n.